viernes, 14 de diciembre de 2012
Final de Trimestre
Este trimestre nos ha parecido bueno porque nos hemos entretenido mucho con nuestro blog. Lo que mas no ha gustado de nuestro blog ha sido la apariencia del blog. Creemos que debemos mejorar las entradas de nuestro blog extendiéndolas mas y haciendo mas entradas.
viernes, 16 de noviembre de 2012
Siemtría
La simetría es un rasgo característico de formas geométricas, sistemas, ecuaciones y otros objetos materiales, o entidades abstractas, relacionada con su invariación bajo ciertas transformaciones, movimientos o intercambios.
Hay varios tipos de simetría, simetría física, geométrica, en biología,pero en realidad solo hemos dado 2 tipos de simetría geométrica:
Hay varios tipos de simetría, simetría física, geométrica, en biología,pero en realidad solo hemos dado 2 tipos de simetría geométrica:
- Simetría reflectiva o simetría especular
que se caracteriza por la existencia de un único plano, matemáticamente
está asociado al grupo SO(1) o su representación equivalente
.
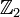En dos dimensiones tiene un eje de simetría y en tres dimensiones tiene
un plano. El eje de simetría de una figura bidimensional es una línea,
si se construye una perpendicular, cualquier punto que reposee en esta
perpendicular a la misma distancia del eje de simetría son idénticos.
Otra manera de verlo es que si la forma se doblara por la mitad sobre el
eje, las dos mitades serían iguales. Por ejemplo, un cuadrado tiene
cuatro ejes de simetría, ya que hay cuatro formas diferentes de doblarlo
haciendo que sus bordes coincidan. Un círculo tendría infinitos ejes de
simetría por la misma razón. - Simetría traslacional se da cuando la transformación
deja invariable a un objeto bajo un grupo de traslaciones discretas o
continuas. El grupo es discreto si la invariancia sólo se da para un
número numerable de valores de a y continuo si la invariancia se presenta para un conjunto infinito no numerable de valores de a en caso contrario.
viernes, 26 de octubre de 2012
¿Que pensais sobre nuestro blog?
Habiendo publicado algunas entradas, participando nosotros nada mas en ellas,queremos que vosotros también participéis y opinéis sobre él. ¿Pensáis en que deberíamos cambiar algo? ¿Que opináis sobre nuestras entradas?
Esperamos vuestros comentarios.
Esperamos vuestros comentarios.
viernes, 19 de octubre de 2012
Libro recomendado
Este libro es un manual práctico de dibujo técnico para aprender sobre las técnicas usadas en el dibujo, también se puede aprender algo de historia del dibujo, la representación de figuras geométricas, de piezas y el manejo de los instrumentos de dibujo entre otras muchas cosas. Un libro fantástico para los aficionados al dibujo técnico.
lunes, 8 de octubre de 2012
Poligonos regulares y estrellados
En geometría, se le llama polígono regular a un polígono cuyos lados y ángulos interiores son congruentes entre sí. Los polígonos regulares de tres y cuatro lados se llaman triángulo equilátero y cuadrado, respectivamente; para polígonos de más lados, se añade el término regular (pentágono regular, hexágono regular, ...). Solo algunos polígonos regulares pueden ser construidos con regla y compás.
En nuestro caso solo hemos hecho y dibujado hasta el eneágono regular:
En nuestro caso solo hemos hecho y dibujado hasta el eneágono regular:
viernes, 28 de septiembre de 2012
El Arco Capaz
El arco capaz es el lugar geométrico de los puntos desde los que un segmento AB se «ve» con el mismo ángulo; es decir, el lugar geométrico de los vértices de los ángulos que tienen la misma amplitud y abarcan un mismo segmento.
El arco capaz de un segmento AB, de ángulo λ, es un arco de circunferencia que contiene el vértice del ángulo λ, y los puntos A y B. El ángulo que subtiende el segmento AB visto desde el centro del círculo es 2λ.
En rigor, el lugar geométrico de los puntos desde los que se ve con un mismo ángulo al segmento AB son dos arcos simétricamente dispuestos respecto del segmento AB.
Arco capaz del ángulo de 90º
El más utilizado es el arco capaz con ángulo λ = 90º. Este caso se corresponde con el 2º teorema de tales, de tal modo que el arco capaz es la circunferencia cuyo diámetro es el segmento AB.
Conocer las propiedades del arco capaz es muy útil en dibujo para resolver problemas geométricos relacionados con ángulos y polígonos.
Fuente: http://es.wikipedia.org/wiki/Arco_capaz
El arco capaz de un segmento AB, de ángulo λ, es un arco de circunferencia que contiene el vértice del ángulo λ, y los puntos A y B. El ángulo que subtiende el segmento AB visto desde el centro del círculo es 2λ.
En rigor, el lugar geométrico de los puntos desde los que se ve con un mismo ángulo al segmento AB son dos arcos simétricamente dispuestos respecto del segmento AB.
El más utilizado es el arco capaz con ángulo λ = 90º. Este caso se corresponde con el 2º teorema de tales, de tal modo que el arco capaz es la circunferencia cuyo diámetro es el segmento AB.
Conocer las propiedades del arco capaz es muy útil en dibujo para resolver problemas geométricos relacionados con ángulos y polígonos.
Fuente: http://es.wikipedia.org/wiki/Arco_capaz
viernes, 21 de septiembre de 2012
Presentación del Blog
Somos Álvaro Pérez y Rafael Yuste y vamos a hacer este blog sobre nuestra asignatura de dibujo técnico. Pondremos todo lo que estamos dando en este curso de 1º de Bachillerato.
Suscribirse a:
Entradas (Atom)